Unlikely

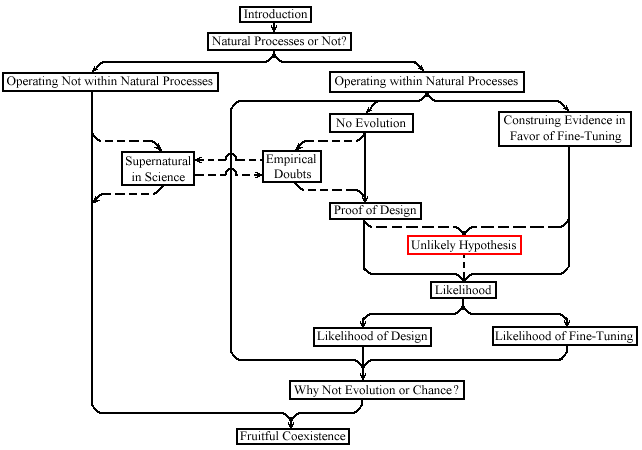
Unlikely Hypothesis

If a hypothesis predicts that an event is very unlikely, and the event happens anyway, can you thereby conclude that the hypothesis was wrong? No. Consider a fair lottery in which 1,000,000 different tickets are sold to 1,000,000 different people. The laws of statistics in conjunction with the assumption that the lottery is fair allow us to predict that the probability of any one person winning is 1 in 1,000,000, a very small probability --- and yet someone does win. Does this event falsify the laws of probability and/or the assumption that the lottery is fair? Not at all. This counterexample shows that if a hypothesis predicts that the probability of an outcome is very low, and yet the outcome does happen, this is not necessarily proof that the hypothesis is incorrect. Given the assumptions, someone or other is going to win; it's just a matter of who.

It may be objected that the assumption that the lottery is fair enforces that some person or other will win with 100% probability, so it is not a good analogy. Yet the argument against blind chance is really about the improbability of a particular outcome within a range of outcomes. The probability that we see a particular universe (such as one in which there is intelligence or delicate adaptations such as eyes) may be very small, given many possible universes where no one universe is much more probable than any other. And yet the universe had to come out some way with 100% probability, even if the probability of it coming out the way it does is very small. Therefore the lottery analogy is a good one: in both cases, the predicted probability of a particular outcome is very low, even though, within the possible range of outcomes, some outcome or other must surely come to pass.

Thus if the argument against chance or evolution attempts to exclude them based on the improbability of this particular universe having delicate adaptations like eyes, it fails. We are no more required to posit an intelligent designer in explaining why there are eyes than we are in explaining why someone wins the lottery. Both events had to come out some way with 100% probability, no matter how improbable any particular outcome is.

All of this is to say, as Elliott Sober (2002b) has pointed out, that there is no analog to modus tollens in probabilistic arguments.

This fact must be kept in mind when considering the probability of outcomes which are composed of the conjunction of many outcomes. If the probability of outcome A is 1 in 10, and the probability of outcome B is 1 in 10, and if outcome A and outcome B are independent, then the probability of outcomes A & B conjoined is 1 in 100 --- the probabilities multiply. This fact makes our prediction of the probability of the conjunction of many outcomes very small --- and yet they do happen. For example, the probability of obtaining a particular sequence of heads and tails in 10 tosses of a fair coin such as: HHTTTHTTTH is

(1/2)(1/2)(1/2)(1/2)(1/2)(1/2)(1/2)(1/2)(1/2)(1/2) = 1/1024

which is the same as the probability of obtaining HHHHHHHHHH or HHHTHHHHHH or HHHHHHHHTT or any particular sequence of heads and tails determined by 10 tosses of a fair coin.

If the statistical argument against blind chance were valid, then we would have to invoke an intelligent designer to explain just about every event that has ever happened. For instance, forget about the watch Paley found in the field --- what are the chances that Paley finds his stone in that particular field, in that particular location, at that particular time, and with that particular composition? If one credits the argument excluding blind chance based on improbability, then one must admit that the whole universe would have to have been very finely tuned or delicately designed indeed to produce the particular outcome of that stone being what it was, how it was, where it was, and when it was!

Now, it must be admitted that the improbability of what we see being the result of chance or evolution, cannot be considered a disproof of the hypothesis that it is the result of chance or evolution. But perhaps it could be seen as something which makes Creationism or Intelligent Design more likely than chance or evolution. For a discussion of that position, go to Likelihood.